Access Answers to Maths NCERT Solutions for Class 7 Chapter 8 – Comparing Quantities

Exercise 8.1 Page: 157

1. Find the ratio of:

(a) ₹ 5 to 50 paise

Solution:-

We know that,

₹ 1 = 100 paise

Then,

₹ 5 = 5 × 100 = 500 paise

Now we have to find the ratio,

= 500/50

= 10/1

So, the required ratio is 10: 1.

(b) 15 kg to 210 g

Solution:-

We know that,

1 kg = 1000 g

Then,

15 kg = 15 × 1000 = 15000 g

Now we have to find the ratio,

= 15000/210

= 1500/21

= 500/7 … [∵divide both by 3]

So, the required ratio is 500: 7.

(c) 9 m to 27 cm

Solution:-

We know that,

1 m = 100 cm

Then,

9 m = 9 × 100 = 900 cm

Now we have to find the ratio,

= 900/27

= 100/3 … [∵divide both by 9]

So, the required ratio is 100: 3.

(d) 30 days to 36 hours

Solution:-

We know that,

1 day = 24 hours

Then,

30 days = 30 × 24 = 720 hours

Now we have to find the ratio,

= 720/36

= 20/1 … [∵divide both by 36]

So, the required ratio is 20: 1.

2. In a computer lab, there are 3 computers for every 6 students. How many computers will be needed for 24 students?

Solution:-

From the question it is given that,

Number of computer required for 6 students = 3

So, number of computer required for 1 student = (3/6)

= ½

So, number of computer required for 24 students = 24 × ½

= 24/2

= 12

∴ Number of computers required for 24 students is 12.

3. Population of Rajasthan = 570 lakhs and population of UP = 1660 lakhs.

Area of Rajasthan = 3 lakh km² and area of UP = 2 lakh km² .

(i) How many people are there per km² in both these states?

(ii) Which state is less populated?

Solution:-

(i) From the question, it is given that,

Population of Rajasthan = 570 lakh

Area of Rajasthan = 3 lakh Km²

Then, population of Rajasthan in 1 km² area = (570 lakh)/ (3 lakh km² )

= 190 people per km²

Population of UP = 1660 Lakh

Area of UP = 2 Lakh km²

Then, population of UP in 1 lakh km² area = (1660 lakh)/ (2 lakh km² )

= 830 people per km²

(ii) By comparing the two states, we find that Rajasthan is the less populated state.

---

Exercise 8.2 Page: 164

1. Convert the given fractional numbers to percent.

(a) 1/8

Solution:-

In order to convert a fraction into a percentage multiply the fraction by 100 and put the percent sign %.

= (1/8) × 100 %

= 100/8 %

= 12.5%

(b) 5/4

Solution:-

In order to convert a fraction into a percentage multiply the fraction by 100 and put the percent sign %.

= (5/4) × 100 %

= 500/4 %

= 125%

(c) 3/40

Solution:-

In order to convert a fraction into a percentage multiply the fraction by 100 and put the percent sign %.

= (3/40) × 100 %

= 300/40 %

= 30/4 %

= 7.5%

(d) 2/7

Solution:-

In order to convert a fraction into a percentage multiply the fraction by 100 and put the percent sign %.

= (2/7) × 100 %

= 200/7 %

=
%

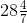2. Convert the given decimal fraction to percent.

(a) 0.65

Solution:-

First we have to remove the decimal point,

= 65/100

Now,

Multiply by 100 and put the percent sign %.

We have,

= (65/100) × 100

= 65%

(b) 2.1

Solution:-

First we have to remove the decimal point,

= 21/10

Now,

Multiply by 100 and put the percent sign %.

We have,

= (21/10) × 100

=210%

(c) 0.02

Solution:-

First we have to remove the decimal point,

= 2/100

Now,

Multiply by 100 and put the percent sign %.

We have,

= (2/100) × 100

= 2%

(d) 12.35

Solution:-

First we have to remove the decimal point,

= 1235/100

Now,

Multiply by 100 and put the percent sign %.

We have,

= (1235/100) × 100)

= 1235%

3. Estimate what part of the figures is coloured, and hence find the per cent which is coloured.

(i)

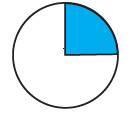
Solution:-

By observing the given figure,

We can identify that 1 part is shaded out of 4 equal parts.

It is represented by a fraction = ¼

Then,

= ¼ × 100

= 100/4

= 25%

Hence, 25% of the figure is coloured.

(ii)

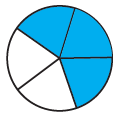
Solution:-

By observing the given figure,

We can identify that 3 parts are shaded out of 5 equal parts.

It is represented by a fraction = 3/5

Then,

= (3/5) × 100

= 300/5

= 60%

Hence, 60% of the figure is coloured.

(iii)

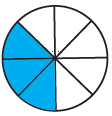
Solution:-

By observing the given figure,

We can identify that 3 parts are shaded out of 8 equal parts.

It is represented by a fraction = 3/8

Then,

= (3/8) × 100

= 300/8

= 37.5%

Hence, 37.5% of the figure is coloured.

4. Find:

(a) 15% of 250

Solution:-

We have,

= (15/100) × 250

= (15/10) × 25

= (15/2) × 5

= (75/2)

= 37.5

(b) 1% of 1 hour

Solution:-

We know that, 1 hour = 60 minutes

Then,

1% of 60 minutes

1 minute = 60 seconds

60 minutes = 60 × 60 = 3600 seconds

Now,

1% of 3600 seconds

= (1/100) × 3600

= 1 × 36

= 36 seconds

(c) 20% of ₹ 2500

Solution:-

We have,

= (20/100) × 2500

= 20 × 25

= ₹ 500

(d) 75% of 1 kg

Solution:-

We know that, 1 kg = 1000 g

Then,

75% of 1000 g

= (75/100) × 1000

= 75 × 10

= 750 g

5. Find the whole quantity if

(a) 5% of it is 600

Solution:-

Let us assume the whole quantity be x,

Then,

(5/100) × (x) = 600

X = 600 × (100/5)

X = 60000/5

X = 12000

(b) 12% of it is ₹ 1080.

Solution:-

Let us assume the whole quantity is x,

Then,

(12/100) × (x) = 1080

X = 1080 × (100/12)

X = 540 × (100/6)

X = 90 × 100

X = ₹ 9000

(c) 40% of it is 500k km

Solution:-

Let us assume the whole quantity is x,

Then,

(40/100) × (x) = 500

X = 500 × (100/40)

X = 500 × (10/4)

X = 500 × 2.5

X = 1250 km

(d) 70% of it is 14 minutes

Solution:-

Let us assume the whole quantity is x,

Then,

(70/100) × (x) = 14

X = 14 × (100/70)

X = 14 × (10/7)

X = 20 minutes

(e) 8% of it is 40 liters

Solution:-

Let us assume the whole quantity is x,

Then,

(8/100) × (x) = 40

X = 40 × (100/8)

X = 40 × (100/8)

X = 40 × 12.5

X = 500 liters

6. Convert given percent to decimal fractions and also fractions in simplest forms:

(a) 25%

Solution:-

First convert the given percentage into fraction and then put the fraction into decimal form.

= (25/100)

= ¼

= 0.25

(b) 150%

Solution:-

First convert the given percentage into fraction and then put the fraction into decimal form.

= (150/100)

= 3/2

= 1.5

(c) 20%

Solution:-

First convert the given percentage into fraction and then put the fraction into decimal form.

= (20/100)

= 1/5

= 0.2

(d) 5%

Solution:-

First convert the given percentage into fraction and then put the fraction into decimal form.

= (5/100)

= 1/20

= 0.05

7. In a city, 30% are females, 40% are males and remaining are children. What per cent are children?

Solution:-

From the question, it is given that

Percentage of female in a city =30%

Percentage of male in a city = 40%

Total percentage of both male and female = 40% + 30%

= 70%

Now we have to find the percentage of children = 100 – 70

= 30%

So, 30% are children.

8. Out of 15,000 voters in a constituency, 60% voted. Find the percentage of voters who did not vote. Can you now find how many actually did not vote?

Solution:-

From the question, it is given that

Total number of voters in the constituency = 15000

Percentage of people who voted in the election = 60%

Percentage of people who did not vote in the election = 100 – 60

= 40%

Total number of voters who did not vote in the election = 40% of 15000

= (40/100) × 15000

= 0.4 × 15000

= 6000 voters

∴ 6000 voters did not vote.

9. Meeta saves ₹ 4000 from her salary. If this is 10% of her salary. What is her salary?

Solution:-

Let us assume Meeta’s salary be ₹ x,

Then,

10% of ₹ x = ₹ 4000

(10/100) × (x) = 4000

X = 4000 × (100/10)

X = 4000 × 10

X = ₹ 40000

∴ Meeta’s salary is ₹ 40000.

10. A local cricket team played 20 matches in one season. It won 25% of them. How many matches did they win?

Solution:-

From the question, it is given that

Total matches played by a local team = 20

Percentage of matches won by the local team = 25%

Then,

Number of matches won by the team = 25% of 20

= (25/100) × 20

= 25/5

= 5 matches.

∴ The local team won 5 matches out of 20 matches.

---

Exercise 8.3 Page: 171

1. Tell what is the profit or loss in the following transactions. Also find profit per cent or loss per cent in each case.

(a) Gardening shears bought for ₹ 250 and sold for ₹ 325.

Solution:-

From the question, it is given that

Cost price of gardening shears = ₹ 250

Selling price of gardening shears = ₹ 325

Since (SP) >(CP), so there is a profit

Profit = (SP) – (CP)

= ₹ (325 – 250)

= ₹ 75

Profit % = {(Profit/CP) × 100}

= {(75/250) × 100}

= {7500/250}

= 750/25

= 30%

(b) A refrigerator bought for ₹ 12,000 and sold at ₹ 13,500.

Solution:-

From the question, it is given that

Cost price of refrigerator = ₹ 12000

Selling price of refrigerator = ₹ 13500

Since (SP) >(CP), so there is a profit

Profit = (SP) – (CP)

= ₹ (13500 – 12000)

= ₹ 1500

Profit % = {(Profit/CP) × 100}

= {(1500/12000) × 100}

= {150000/12000}

= 150/12

= 12.5%

(c) A cupboard was bought for ₹ 2,500 and sold at ₹ 3,000.

Solution:-

From the question, it is given that

Cost price of cupboard = ₹ 2500

Selling price of cupboard = ₹ 3000

Since (SP) >(CP), so there is a profit

Profit = (SP) – (CP)

= ₹ (3000 – 2500)

= ₹ 500

Profit % = {(Profit/CP) × 100}

= {(500/2500) × 100}

= {50000/2500}

= 500/25

= 20%

(d) A skirt was bought for ₹ 250 and sold at ₹ 150.

Solution:-

Since (SP) <(CP), so there is a loss

Loss = (CP) – (SP)

= ₹ (250 – 150)

= ₹ 100

Loss % = {(Loss/CP) × 100}

= {(100/250) × 100}

= {10000/250}

= 40%

2. Convert each part of the ratio to percentage:

(a) 3 : 1

Solution:-

We have to find total parts by adding the given ratio = 3 + 1 = 4

1^st part = ¾ = (¾) × 100 %

= 3 × 25%

= 75%

2^nd part = ¼ = (¼) × 100%

= 1 × 25

= 25%

(b) 2: 3: 5

Solution:-

We have to find total parts by adding the given ratio = 2 + 3 + 5 = 10

1^st part = 2/10 = (2/10) × 100 %

= 2 × 10%

= 20%

2^nd part = 3/10 = (3/10) × 100%

= 3 × 10

= 30%

3^rd part = 5/10 = (5/10) × 100%

= 5 × 10

= 50%

(c) 1:4

Solution:-

We have to find total parts by adding the given ratio = 1 + 4 = 5

1^st part = (1/5) = (1/5) × 100 %

= 1 × 20%

= 20%

2^nd part = (4/5) = (4/5) × 100%

= 4 × 20

= 80%

(d) 1: 2: 5

Solution:-

We have to find total parts by adding the given ratio = 1 + 2 + 5 = 8

1^st part = 1/8 = (1/8) × 100 %

= (100/8) %

= 12.5%

2^nd part = 2/8 = (2/8) × 100%

= (200/8)

= 25%

3^rd part = 5/8 = (5/8) × 100%

= (500/8)

= 62.5%

3. The population of a city decreased from 25,000 to 24,500. Find the percentage decrease.

Solution:-

From the question, it is given that

Initial population of the city = 25000

Final population of the city = 24500

Population decrease = Initial population – Final population

= 25000 – 24500

= 500

Then,

Percentage decrease in population = (population decrease/Initial population) × 100

= (500/25000) × 100

= (50000/25000)

= 50/25

= 2%

4. Arun bought a car for ₹ 3,50,000. The next year, the price went upto ₹ 3,70,000. What was the percentage of price increase?

Solution:-

From the question, it is given that

Arun bought a car for = ₹ 350000

The price of the car in the next year, went up to = ₹ 370000

Then increase in price of car = ₹ 370000 – ₹ 350000

= ₹ 20000

The percentage of price increase = (₹ 20000/ ₹ 350000) × 100

= (2/35) × 100

= 200/35

= 40/7

=

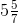
5. I buy a T.V. for ₹ 10,000 and sell it at a profit of 20%. How much money do I get for it?

Solution:-

From the question, it is given that

Cost price of the T.V. = ₹ 10000

Percentage of profit = 20%

Profit = (20/100) × 10000

= ₹ 2000

Then,

Selling price of the T.V. = cost price + profit

= 10000 + 2000

= ₹ 12000

∴ I will get it for ₹ 12000.

6. Juhi sells a washing machine for ₹ 13,500. She loses 20% in the bargain. What was the price at which she bought it?

Solution:-

From the question, it is given that

Selling price of washing machine = ₹ 13500

Percentage of loss = 20%

Now, we have to find the cost price washing machine

By using the formula, we have:

CP = ₹ {(100/ (100 – loss %)) × SP}

= {(100/ (100 – 20)) × 13500}

= {(100/ 80) × 13500}

= {1350000/80}

= {135000/8}

= ₹ 16875

7. (i) Chalk contains calcium, carbon and oxygen in the ratio 10:3:12. Find the percentage of carbon in chalk.

Solution:-

From the question it is given that,

The ratio of calcium, carbon and oxygen in chalk = 10: 3: 12

So, total part = 10 + 3 + 12 = 25

In that total part amount of carbon = 3/25

Then,

Percentage of carbon = (3/25) × 100

= 3 × 4

= 12 %

(ii) If in a stick of chalk, carbon is 3g, what is the weight of the chalk stick?

Solution:-

From the question it is given that,

Weight of carbon in the chalk = 3g

Let us assume the weight of the stick be x

Then,

12% of x = 3

(12/100) × (x) = 3

X = 3 × (100/12)

X = 1 × (100/4)

X = 25g

∴The weight of the stick is 25g.

8. Amina buys a book for ₹ 275 and sells it at a loss of 15%. How much does she sell it for?

Solution:-

From the question, it is given that

Cost price of book = ₹ 275

Percentage of loss = 15%

Now, we have to find the selling price book,

By using the formula, we have:

SP = {((100 – loss %) /100) × CP)}

= {((100 – 15) /100) × 275)}

= {(85 /100) × 275}

= 23375/100

= ₹ 233.75

9. Find the amount to be paid at the end of 3 years in each case:

(a) Principal = ₹ 1,200 at 12% p.a.

Solution:-

Given: – Principal (P) = ₹ 1200, Rate (R) = 12% p.a. and Time (T) = 3years.

If interest is calculated uniformly on the original principal throughout the loan period, it is called Simple Interest (SI).

SI = (P × R × T)/100

= (1200 × 12 × 3)/ 100

= (12 × 12 × 3)/ 1

= ₹432

Amount = (Principal + SI)

= (1200 + 432)

= ₹ 1632

(b) Principal = ₹ 7,500 at 5% p.a.

Solution:-

Given: – Principal (P) = ₹ 7500, Rate (R) = 5% p.a. and Time (T) = 3years.

If interest is calculated uniformly on the original principal throughout the loan period, it is called Simple Interest (SI).

SI = (P × R × T)/100

= (7500 × 5 × 3)/ 100

= (75 × 5 × 3)/ 1

= ₹ 1125

Amount = (Principal + SI)

= (7500 + 1125)

= ₹ 8625

10. What rate gives ₹ 280 as interest on a sum of ₹ 56,000 in 2 years?

Solution:-

Given: – P = ₹ 56000, SI = ₹ 280, t = 2 years.

We know that,

R = (100 × SI) / (P × T)

= (100 × 280)/ (56000 × 2)

= (1 × 28) / (56 × 2)

= (1 × 14) / (56 × 1)

= (1 × 1) / (4 × 1)

= (1/ 4)

= 0.25%

11. Meena gives an interest of ₹ 45 for one year at 9% rate p.a. What is the sum she has borrowed?

Solution:-

From the question it is given that, SI = ₹ 45, R = 9%, T = 1 year, P =?

SI = (P × R × T)/100

45 = (P × 9 × 1)/ 100

P = (45 ×100)/ 9

= 5 × 100

= ₹ 500

Hence, she borrowed ₹ 500.

---